How To Find Asymptotes Of A Rational Function

Show General Find Show Mobile Find Show All NotesHide All Notes

General Notice

Surprise update today. I was going to hold off on this for a few weeks while I worked on a couple of other things but decided to go ahead and push a couple of changes to the website today as the balance of the changes were all behind the scenes, so to speak, and shouldn't (fingers crossed) have an impact on the site or people using information technology.

First, and most noticeable, is a change to a "fixed width" content area simply to make the website a little more "consistent" on about desktop/laptop monitors. I besides added a piddling space between lines of text. Hopefully these changes will make the site a fiddling easier to read. Annotation that y'all may need to clear your browser enshroud to get this change to display right away.

Adjacent, for a variety of reasons I take stopped offer pdf downloads of individual sections and chapters for those using that feature. Without going into cracking item on the decision I am making a change to the "source" documents that will make generating affiliate/section pdf'south much more difficult while at the same fourth dimension making it easier to generate the full book pdf and (hopefully) finally permit me to have "links" to other sections of the volume exist agile in the pdf files.

At the nowadays fourth dimension, and for the foreseeable hereafter, any current link to a affiliate or section pdf file will non pause but will redirect to download the total book pdf instead of the chapter/department file and the actual pdf files for the capacity/sections will exist removed from the website.

Paul
March 1, 2022

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.eastward. yous are probably on a mobile telephone). Due to the nature of the mathematics on this site it is best views in mural mode. If your device is not in mural mode many of the equations volition run off the side of your device (should be able to scroll to see them) and some of the bill of fare items volition be cut off due to the narrow screen width.

Section four-8 : Rational Functions

In this concluding section we demand to talk over graphing rational functions. Information technology's is probably all-time to start off with a fairly simple one that we tin do without all that much knowledge on how these work.

Let'due south sketch the graph of \(f\left( ten \correct) = \frac{i}{10}\). Starting time, since this is a rational function we are going to have to be careful with division by cypher issues. So, nosotros can encounter from this equation that nosotros'll accept to avert \(ten = 0\) since that will give division past zero.

Now, let's just plug in some values of \(x\) and see what we get.

\(ten\)	\(f(x)\)
-4	-0.25
-ii	-0.5
-1	-ane
-0.1	-10
-0.01	-100
0.01	100
0.one	10
1	1
2	0.5
4	0.25

So, as \(ten\) get large (positively and negatively) the function keeps the sign of \(ten\) and gets smaller and smaller. As well, as we arroyo \(x = 0\) the function once again keeps the aforementioned sign as \(x\) simply starts getting quite large. Here is a sketch of this graph.

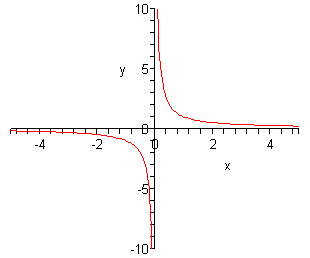
First, detect that the graph is in 2 pieces. Nearly all rational functions volition have graphs in multiple pieces like this.

Adjacent, observe that this graph does non have any intercepts of any kind. That'south easy enough to check for ourselves.

Retrieve that a graph will have a \(y\)-intercept at the point \(\left( {0,f\left( 0 \right)} \right)\). Yet, in this case we have to avoid \(x = 0\) and and so this graph will never cross the \(y\)-axis. Information technology does get very close to the \(y\)-centrality, but it will never cross or touch it and so no \(y\)-intercept.

Adjacent, think that we can determine where a graph will accept \(10\)-intercepts by solving \(f\left( x \correct) = 0\). For rational functions this may seem like a mess to deal with. Nonetheless, there is a nice fact about rational functions that we can use here. A rational office will be zero at a particular value of \(x\) only if the numerator is zero at that \(x\) and the denominator isn't zilch at that \(x\). In other words, to determine if a rational function is ever zero all that we need to exercise is prepare the numerator equal to zero and solve. Once we have these solutions we but demand to check that none of them make the denominator zero besides.

In our case the numerator is one and will never be aught and then this function volition take no \(x\)-intercepts. Again, the graph will get very close to the \(x\)-axis merely it will never touch or cantankerous it.

Finally, we need to address the fact that graph gets very close to the \(ten\) and \(y\)-axis only never crosses. Since there isn't anything special virtually the axis themselves we'll use the fact that the \(ten\)-centrality is actually the line given past \(y = 0\) and the \(y\)-axis is really the line given by \(x = 0\).

In our graph as the value of \(ten\) approaches \(x = 0\) the graph starts gets very large on both sides of the line given by \(ten = 0\). This line is called a vertical asymptote.

Also, every bit \(x\) get very large, both positive and negative, the graph approaches the line given by \(y = 0\). This line is called a horizontal asymptote.

Here are the full general definitions of the two asymptotes.

1. The line \(10 = a\) is a vertical asymptote if the graph increases or decreases without bound on ane or both sides of the line as \(x\) moves in closer and closer to \(x = a\).
2. The line \(y = b\) is a horizontal asymptote if the graph approaches \(y = b\) as \(x\) increases or decreases without bound. Annotation that it doesn't have to approach \(y = b\) equally \(x\) BOTH increases and decreases. It only needs to approach it on one side in order for it to exist a horizontal asymptote.

Determining asymptotes is actually a fairly simple procedure. First, let's showtime with the rational function,

\[f\left( x \right) = \frac{{a{x^n} + \cdots }}{{b{10^k} + \cdots }}\]

where \(n\) is the largest exponent in the numerator and \(m\) is the largest exponent in the denominator.

We then have the post-obit facts well-nigh asymptotes.

1. The graph will take a vertical asymptote at \(x = a\) if the denominator is zero at \(x = a\) and the numerator isn't nix at \(10 = a\).
2. If \(northward < k\) then the \(x\)-axis is the horizontal asymptote.
3. If\(n = yard\) then the line \(\displaystyle y = \frac{a}{b}\) is the horizontal asymptote.
4. If \(n > m\) there will exist no horizontal asymptotes.

The procedure for graphing a rational role is fairly simple. Here it is.

Process for Graphing a Rational Function

1. Find the intercepts, if at that place are whatsoever. Recollect that the \(y\)-intercept is given by \(\left( {0,f\left( 0 \right)} \right)\) and we find the \(x\)-intercepts by setting the numerator equal to zero and solving.
2. Find the vertical asymptotes by setting the denominator equal to zero and solving.
3. Find the horizontal asymptote, if information technology exists, using the fact above.
4. The vertical asymptotes will divide the number line into regions. In each region graph at to the lowest degree one indicate in each region. This point will tell u.s. whether the graph will exist above or below the horizontal asymptote and if we need to we should get several points to make up one's mind the general shape of the graph.
5. Sketch the graph.

Note that the sketch that we'll get from the process is going to be a fairly crude sketch but that is okay. That's all that nosotros're really after is a basic idea of what the graph will look at.

Let's take a look at a couple of examples.

Example 1 Sketch the graph of the post-obit office. \[f\left( 10 \right) = \frac{{3x + vi}}{{ten - 1}}\]

Evidence Solution

So, we'll start off with the intercepts. The \(y\)-intercept is,

\[f\left( 0 \correct) = \frac{6}{{ - 1}} = - 6\hspace{0.25in} \Rightarrow \hspace{0.25in}\left( {0, - 6} \correct)\]

The \(x\)-intercepts will be,

\[\begin{align*}3x + 6 & = 0\\ x & = - 2\hspace{0.25in} \Rightarrow \hspace{0.25in}\left( { - 2,0} \right)\end{align*}\]

Now, we need to determine the asymptotes. Let's showtime find the vertical asymptotes.

\[x - i = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}x = i\]

So, we've got 1 vertical asymptote. This ways that there are now ii regions of \(ten\)'s. They are \(x < 1\) and \(x > ane\).

At present, the largest exponent in the numerator and denominator is ane and so by the fact in that location will be a horizontal asymptote at the line.

\[y = \frac{3}{1} = iii\]

Now, nosotros just need points in each region of \(ten\)'s. Since the \(y\)-intercept and \(ten\)-intercept are already in the left region we won't demand to go whatever points at that place. That means that nosotros'll just need to get a indicate in the correct region. It doesn't really affair what value of \(x\) nosotros pick here we just need to keep it adequately small then it volition fit onto our graph.

\[f\left( 2 \right) = \frac{{3\left( 2 \right) + half dozen}}{{2 - ane}} = \frac{{12}}{1} = 12\hspace{0.25in} \Rightarrow \hspace{0.25in}\left( {two,12} \right)\]

Okay, putting all this together gives the following graph.

Annotation that the asymptotes are shown every bit dotted lines.

Instance 2 Sketch the graph of the post-obit office. \[f\left( x \right) = \frac{9}{{{10^ii} - ix}}\]

Show Solution

Okay, we'll start with the intercepts. The \(y\)-intercept is,

\[f\left( 0 \right) = \frac{ix}{{ - 9}} = - 1\hspace{0.25in} \Rightarrow \hspace{0.25in}\left( {0, - 1} \right)\]

The numerator is a constant and so there won't be any \(x\)-intercepts since the role can never be zero.

Side by side, we'll have vertical asymptotes at,

\[{x^two} - 9 = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}x = \pm 3\]

So, in this case we'll have three regions to our graph : \(x < - 3\), \( - three < 10 < iii\), \(x > three\).

Too, the largest exponent in the denominator is 2 and since in that location are no \(x\)'s in the numerator the largest exponent is 0, then by the fact the \(x\)-axis will be the horizontal asymptote.

Finally, we demand some points. Nosotros'll apply the following points here.

\[\brainstorm{align*}f\left( { - 4} \right) & = \frac{9}{7} & \hspace{0.25in} & \left( { - four,\frac{9}{7}} \right)\\ f\left( { - 2} \right) & = - \frac{9}{five} & \hspace{0.25in} & \left( { - 2, - \frac{ix}{5}} \right)\\ f\left( 2 \correct) & = - \frac{9}{five} & \hspace{0.25in} & \left( {ii, - \frac{9}{five}} \correct)\\ f\left( iv \right) & = \frac{9}{7} & \hspace{0.25in} & \left( {4,\frac{9}{7}} \right)\terminate{marshal*}\]

Discover that along with the ­\(y\)-intercept we really have iii points in the eye region. This is considering there are a couple of possible behaviors in this region and we'll need to determine the actual behavior. Nosotros'll encounter the other main behaviors in the next examples and then this volition make more sense at that point.

Here is the sketch of the graph.

Example 3 Sketch the graph of the following part. \[f\left( x \correct) = \frac{{{x^2} - 4}}{{{10^two} - 4x}}\]

Testify Solution

This time find that if we were to plug in \(x = 0\) into the denominator we would get division past aught. This ways there will non be a \(y\)-intercept for this graph. We have however, managed to observe a vertical asymptote already.

Now, let's encounter if we've got \(10\)-intercepts.

\[{10^2} - 4 = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}x = \pm ii\]

So, we've got 2 of them.

We've got one vertical asymptote, but at that place may be more and then let's get through the process and see.

\[{x^2} - 4x = x\left( {10 - four} \correct) = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}x = 0,\,\,x = 4\]

So, we've got two again and the iii regions that nosotros've got are \(10 < 0\), \(0 < x < four\) and \(x > four\).

Next, the largest exponent in both the numerator and denominator is 2 and then by the fact there will exist a horizontal asymptote at the line,

\[y = \frac{1}{1} = 1\]

Now, ane of the \(x\)-intercepts is in the far left region so we don't need whatever points at that place. The other \(x\)-intercept is in the middle region. And then, nosotros'll need a indicate in the far right region and equally noted in the previous instance we will desire to go a couple more points in the heart region to completely determine its behavior.

\[\begin{align*}f\left( 1 \right) & = 1 & \hspace{0.25in} & \left( {1,ane} \correct)\\ f\left( three \right) & = - \frac{v}{3} & \hspace{0.25in} & \left( {3, - \frac{5}{3}} \right)\\ f\left( 5 \right) & = \frac{{21}}{5} & \hspace{0.25in} & \left( {five,\frac{{21}}{five}} \right)\terminate{align*}\]

Here is the sketch for this function.

Notice that this fourth dimension the heart region doesn't have the same behavior at the asymptotes as we saw in the previous example. This can and volition happen fairly oft. Sometimes the behavior at the two asymptotes will exist the aforementioned as in the previous instance and sometimes information technology will take the opposite behavior at each asymptote as we see in this example. Because of this we volition always demand to get a couple of points in these types of regions to determine just what the behavior volition be.

Source: https://tutorial.math.lamar.edu/classes/alg/graphrationalfcns.aspx

Posted by: benoithoughle.blogspot.com

Share this post