how to find inflection points of a function

AP Calculus Review: Inflection Points

By on August 18, 2017 in AP

What are inflection points, and how do you find them? This commodity explains what y'all need to know about inflection points for the AP Calculus exams.

Inflection Points and Concavity

An inflection point is a betoken in a graph at which the concavity changes.

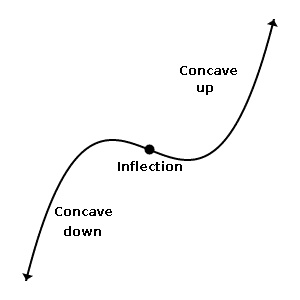
This graph shows a alter in concavity, from concave downwardly to concave upwardly. The inflection point is where the transition occurs.

So let's talk a little well-nigh concavity first.

Concavity

Concavity is nearly curving.

We say that a role y = f(10) is concave up (CU) on a given interval if the graph of the role e'er lies above its tangent lines on that interval. In other words, if you draw a tangent line at any given point, then the graph seems to curve upward, away from the line.

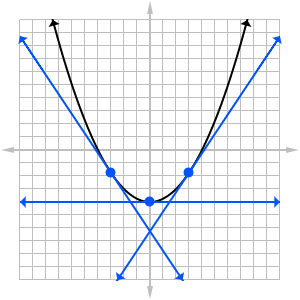
This graph is concave upwardly. At each indicate, the graph curves upward, abroad from its tangent line.

Conversely, a office is concave down (CD) on a given interval if the graph of the function e'er lies below its tangent lines on that interval. That is the graph seems to curve down, away from its tangent line at any given indicate.

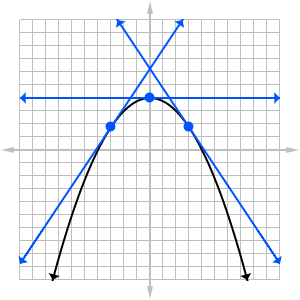
This graph is concave down. At each point, the graph curves downward, away from its tangent line.

This saying may aid you to remember which one is which: Concave up looks like a cup; concave downward looks like a frown.

Inflection

Some functions, like the parabolas shown above, simply have one kind of concavity. But more interesting functions may have a mixture of the ii. The graph might be concave downward in 1 interval and concave up in the next. Some functions even switch dorsum and forth betwixt concave up and concave downwards infinitely many times!

Whatever point at which concavity changes (from CU to CD or from CD to CU) is call an inflection bespeak for the function.

For example, a parabola f(x) = ax ² + bx + c has no inflection points, because its graph is e'er concave upwards or concave downwards.

Inflection Points and Derivatives

Inflection points may exist difficult to spot on the graph itself. So nosotros must rely on calculus to find them.

Basically, it boils down to the 2d derivative.

• If f '' > 0 on an interval, then f is concave up on that interval.
• If f '' < 0 on an interval, and so f is concave down on that interval.
• If f '' changes sign (from positive to negative, or from negative to positive) at a point x = c, and then there is an inflection point located at ten = c on the graph. In particular, the point (c, f(c)) is an inflection indicate for the role f.

Hither'south a practiced dominion of thumb. Look for possible inflection points by setting f '' = 0. That's because the but way for f '' to change signs is to pass through the "neutral territory" of 0 (well, bold the change is continuous, anyhow).

Why the Second Derivative?

So what's so special about the 2nd derivative that makes it the go-to tool for concavity and inflection?

It all has to do with change — in this case, the changing slope of a graph as it curves upward or downwards.

In club for the graph to exist concave up, information technology must ever increase slope as it progresses from left to right. Now call up, the commencement derivative measures slope. So f ' must be increasing whenever the graph is concave upward. The final slice of the puzzle is the observation that increasing functions take positive derivatives. Therefore, the derivative of f ', that is, f '', must exist positive!

Analogously, if the graph is concave downward, then f ' must exist a decreasing part. Hence, concave down means that f '' must be negative.

Finding Inflection Points

Let's come across by example how to locate the inflection points of a graph. Along the fashion, we'll detect out where the function is concave up and concave down.

Let 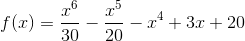. Find all points of inflection and intervals of concavity for f.

Solution

Our kickoff task is to find the commencement and second derivatives.

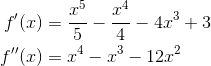
Next, ready the second derivative equal to null and solve. Considering f '' is a polynomial, we have to gene it to discover its roots.

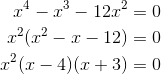
In that location are three solutions, x = 0, 4, and -3. These are non necessarily all going to be inflection points, though! We have to find out how the concavity changes from interval to interval starting time.

Let's set up tabular array to effigy out what happens in each interval. Inside each interval, choose a sample point to plug into f '' to decide the concavity.

Interval	Sample	f ''	Concavity
(-∞, -3)	-iv	128 (> 0)	CU
(-iii, 0)	-ane	-10 (< 0)	CD
(0, four)	ane	-12 (< 0)	CD
(4, ∞)	5	200 (> 0)	CU

Therefore, the function is concave upward on (-∞, -three) U (4, ∞). Information technology's concave down on (-iii, 0) U (0, iv). Notice that in that location is no alter in concavity at x = 0.

That means that the only inflection points are at x = -iii and 4. Plug each of those points into the original part f(ten) to detect their corresponding y-coordinates. (A calculator can help out greatly here!)

• f(-3) = -33.55
• f(4) = -138.67

Thus the two inflection points for this part are: (-three, -33.55) and (iv, -138.67). Let'due south take a await at the graph and see if we can spot how the concavity changes at those points.

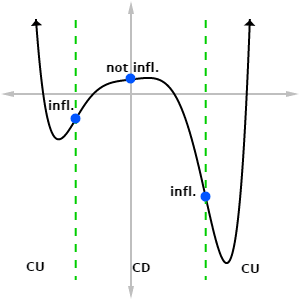
Graph of y = x^6/30 – ten^5/20 – x^4 + 3x + 20, showing intervals of concavity and inflection points. The greenish vertical lines are not part of the graph, but show where concavity changes.

Summary

• An inflection point is a point on the graph of a function at which the concavity changes.
• Points of inflection can occur where the second derivative is zero. In other words, solve f '' = 0 to notice the potential inflection points.
• Even if f ''(c) = 0, you can't conclude that in that location is an inflection at x = c. First you have to determine whether the concavity actually changes at that indicate.

For more data most concavity, inflections, and other related topics, bank check out AP Calculus Review: Functions and their Graphs

• 

  Shaun earned his Ph. D. in mathematics from The Ohio State University in 2008 (Go Bucks!!). He received his BA in Mathematics with a pocket-size in computer science from Oberlin College in 2002. In improver, Shaun earned a B. Mus. from the Oberlin Conservatory in the aforementioned year, with a major in music composition. Shaun still loves music -- almost as much as math! -- and he (thinks he) can play piano, guitar, and bass. Shaun has taught and tutored students in mathematics for about a decade, and hopes his experience can assistance you to succeed!

  View all posts

By the way, Magoosh can assist you study for both the Sabbatum and ACT exams. Click here to learn more!

Source: https://magoosh.com/hs/ap/ap-calculus-review-inflection-points/#:~:text=An%20inflection%20point%20is%20a%20point%20on%20the%20graph%20of,an%20inflection%20at%20x%20%3D%20c.

Posted by: benoithoughle.blogspot.com

Share this post