how to find the slope of the tangent line
4.2: Slope of Tangent Line
- Folio ID
- 1243
Kevin is learning near the basis of calculus and what calculus is actually used for. Unfortunately, Kevin does not understand why calculus is sometimes necessary to find the equation of a line. In Algebra 1, he learned you lot tin find the equation of a line if you are given ii points. You lot observe the slope of the line by dividing the up/downward difference in the points by the left/right difference, then you use one of the points and the gradient to find the y-intercept.
Kevin'due south instructor, Mr. Banner, offered him actress credit if he could find the slope of a line for the points (4,v) and (4,5) using the method he learned in Algebra 1. Can you see what Mr. Imprint did? What is Kevin going to find as he works on those problems?
Tangents to a Curve
Call back from algebra, if points P ( x 0, y 0) and Q ( x ane, y 1) are two dissimilar points on the curve y = f ( ten ), then the slope of the secant line connecting the ii points is given by
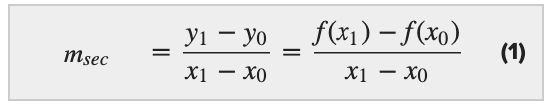
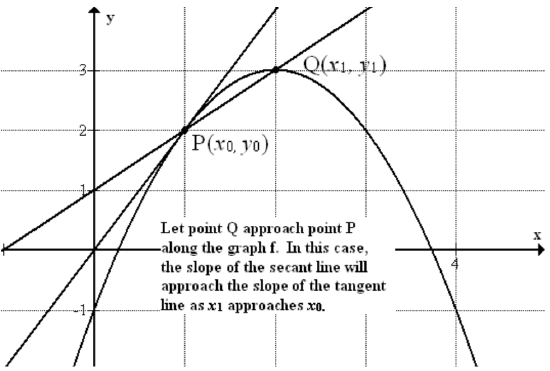
Of course, if we let the indicate x i approach 10 o so Q volition approach P along the graph f and thus the slope of the secant line volition gradually approach the slope of the tangent line every bit 10 1 approaches ten 0. Therefore, (one) becomes
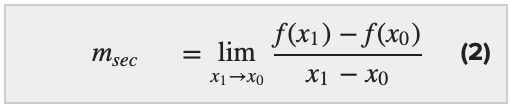
To simplify our notation, if we allow h = ten 1 − x 0, and so 10 1 = x 0 + h and ten1 → x0 becomes equivalent to h → 0. This means that (2) becomes
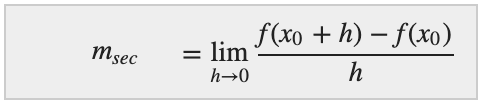
Call back that the equation of the tangent line through point ( x 0, y 0) with slope m is the point-slope form of a line: y − y 0 = m tan( x − x 0).
Examples
Example i
Earlier, y'all were given a problem almost Kevin, who is having trouble understanding calculus.
Mr. Banner asked Kevin to find the equation of a line given the points (iv,5) and (iv,5). The points (4, v) and (4, five) are the same, then the rise/run would exist 00 - Kevin was just introduced to the demand for differential calculus!
Instance 2
Notice line tangent to the curve f ( ten ) = x 3 that passes through point P (two,viii).
Since P ( 10 0, y 0) = (two, 8), using the slope of the tangent equation nosotros have
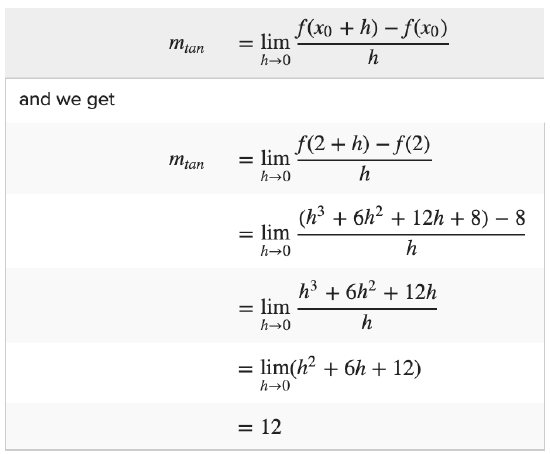
Thus the gradient of the tangent line is 12. Using the bespeak-gradient formula above, we find that the equation of the tangent line is y - 8 = 12 ( x - 2) or y = 12 x - 16.
Instance 3
If f ( x ) = 10 2 − three,discover f' ( x ) and use the result to observe the slope of the tangent line at ten = 2 and x = −ane.
Since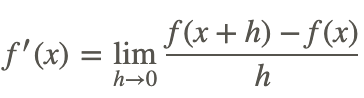 
then
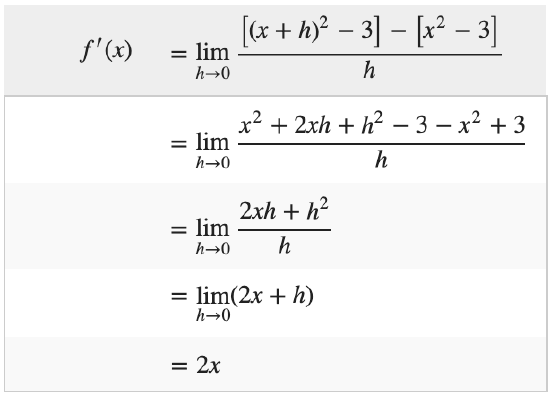
To find the slope, nosotros merely substitute x = 2 into the upshot f' ( 10 ):
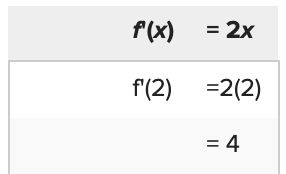
and
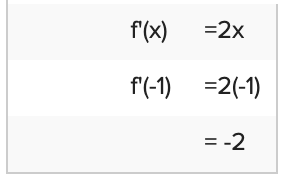
Thus slope of the tangent line at x = ii and x = −one are 4 and −2 respectively.
Example 4
Find the slope of the tangent line to the curve y = 1/ ten that passes through the point (i, 1).
Using the slope of the tangent formula,
Thus the slope of the tangent line at 10 = 1 for the bend y = 1/ x is 1000 = −1. To find the equation of the tangent line, we simply use the point-slope formula,
So the equation of the tangent line is y = - x + ii.
Example 5
Given the function y=1/iix2 and the values of 100=3 and tenane=4, find:
- The boilerplate rate of change of y with respect to x over the interval [ x 0, x i].
Identify the two points past substituting iii and 4 in for x in the office f(x)=1/iix2
Substitute the ii points (3, 4.5) and (4, 8) into the average charge per unit of change formula: g=y1−y0 /xi−x0
Average rate of change = 7/two
- The slope of the secant line connecting x 0 and 10 ane.
The gradient of the secant line between ten0 and x1 is the slope between (3,iv.v) and (4,viii), which is 72.
- The instantaneous rate of change of y with respect to x at x 0.
Instantaneous rate of change is the slope at ten = three.
Use the formula: f(10+h)−f(x)/h where f(10)=ane/2x2 and x=3
f(3+h)−f(3)/h ..... Substitute three for x
0.5(three+h)2−0.5(3)two/h ..... Replace f(ten)→1/2x2
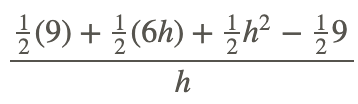
FOIL and Distribute the 1/2
The slope of the tangent at 4 is the same as the instantaneous rate of change at ten=4
This is the same series of steps as with ten = 3 above
∴ the slope at x = 4 is 4
Instance half dozen
Given the function f(x)=1x and the values x0=2 and 101=iii, find:
- The boilerplate charge per unit of change of y with respect to x over the interval [ x 0, 10 one].
Identify the two points by substituting two and 3 in for x in the function
Substitute the ii points (2,ane/2)|(3,1/3) into the boilerplate charge per unit of change formula: m=y1−y0 /xi−ten0
Boilerplate charge per unit of change = −16
- The slope of the secant line connecting x 0 and x ane.
The slope of the secant line betwixt x0 and x1 is the slope between (2,1/two) and (iii,i/3), which is −16.
- The instantaneous rate of modify of y with respect to x at ten 0.
Instantaneous rate of change at 10 0 is the slope at x = 2.
Use the formula: f(x+h)−f(10)/h where f(x)=1/x and ten=2
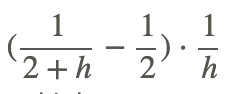We had a fraction divided by a fraction, capsize to multiply
The slope of the tangent at 3 is the same every bit the instantaneous rate of alter at x=three
This is the same series of steps every bit with 10 = 2 above
∴ the slope at ten = iii is −1/9
Review
- What is the line connecting 2 points (x0,y0) and (teni,y1) on a curve chosen?
- Every bit (x0,y0) gets immeasurably close to (xane,y1) the term describing the line between them becomes: "the ____________ line"
- The expression f(x0+h)−f(x0) is used to describe what altitude in the process of finding the slope of a tangent line?
- When computing the gradient of a tangent, what value is assumed to go to 0 as the two called points go closer and closer?
- What does the concept of limit, discussed in prior lessons, have to do with finding the slope of a line tangent to a curve?
Notice the equation of the tangent line:
- What is the equation of the tangent line at x=−3 assuming that r(−three)=−v and r′(−3)=1?
- What is the equation of the tangent line at x=ane assuming that r(1)=3 and r′(1)=−v?
- What is the equation of the tangent line at x=2 assuming that g(ii)=1 and yard′(2)=−iii?
- What is the equation of the tangent line at x=4 assuming that u(iv)=4 and u′(four)=iii?
- What is the equation of the tangent line at x=−4 assuming that t(−4)=2 and t′(−4)=5?
Find the equation of the tangent line:
- Observe the equation of the tangent line to the graph of h(10)=−5xiii−3x2+ten+3 at x=one
- Find the equation of the tangent line to the graph of t(ten)=−2x at 10=−2
- Find the equation of the tangent line to the graph of thou(x)=3x3+3x2+4x+4 at ten=1
- Detect the equation of the tangent line to the graph of q(x)=−x3−4x2+4x+3 at x=−2
- Find the equation of the tangent line to the graph of t(x)=−4x2+2x−4 at ten=−i
- Find the equation of the tangent line to the graph of h(x)=−4x3+2x2−3x+3 at 10=−1
- Find the equation of the tangent line to the graph of m(x)=x at x=0
- Find the equation of the tangent line to the graph of s(x)=−3x2−2x+3 at 10=0
- Find the equation of the tangent line to the graph of c(ten)=−3 at x=0
- Discover the equation of the tangent line to the graph of b(ten)=−5x4+3x3−x2+5x−iii at x=−ane
Review (Answers)
To see the Review answers, open this PDF file and look for department 8.seven.
Vocabulary
| Term | Definition |
|---|---|
| secant | A line that intersects a circle in 2 points. |
| tangent | A line that intersects a circle in exactly 1 indicate. |
| Boilerplate charge per unit of change | The average rate of alter of a function is the alter in y coordinates of a part, divided past the change in x coordinates. |
| Differential calculus | Differential calculus is the branch of calculus based on finding the difference in location between two points that become closer together until the distance between them is infinitely pocket-sized. |
| instantaneous rate of alter | The instantaneous rate of change of a curve at a given signal is the slope of the line tangent to the curve at that signal. |
| secant line | A secant line is a line that joins two points on a curve. |
| Slope | Slope is a measure of the steepness of a line. A line can have positive, negative, goose egg (horizontal), or undefined (vertical) slope. The slope of a line can exist found by calculating "rise over run" or "the change in the y over the change in the x." The symbol for gradient is one thousand |
| Tangent line | A tangent line is a line that "only touches" a bend at a single bespeak and no others. |
Additional Resources
PLIX: Play, Learn, Interact, eXplore - Slope of the Tangent and Secant Lines
Video: Equation of a Tangent Line
Practice: Slope of Tangent Line
Real World: Off the Curve
Source: https://k12.libretexts.org/Bookshelves/Mathematics/Calculus/04%3A_Differentiation_-_Slope_Models_using_Derivatives/4.02%3A_Slope_of_Tangent_Line
Posted by: benoithoughle.blogspot.com
0 Response to "how to find the slope of the tangent line"
Post a Comment